آموزش الگوریتم مرتب سازی هرمی (Heap) + نمونه کد

نویسنده : nivad
ارسال شده در: 5 می 2025
ارسال دیدگاه: 0

آموزش الگوریتم مرتب سازی هرمی (Heap) + نمونه کد

سلام رفقا! امروز می‌خوایم یه الگوریتم مرتب‌سازی خیلی باحال و کاربردی رو با هم یاد بگیریم: مرتب سازی هرمی (Heap Sort). شاید اسمش یکم ترسناک به نظر بیاد، ولی قول میدم آخر این پست، قشنگِ قشنگ براتون جا میفته و می‌تونید ازش تو پروژه‌هاتون استفاده کنید. اصلا نگران نباشید، زبونمون خودمونیه و هر جا لازم باشه، با مثال‌های ساده و عکس‌های خوشگل، قضیه رو باز می‌کنیم. پس کمربندها رو ببندید، بریم که شروع کنیم!

چرا مرتب سازی هرمی مهمه؟

قبل از اینکه بریم سراغ خود الگوریتم، بذارید یه کوچولو راجع به اهمیتش صحبت کنیم. توی دنیای کامپیوتر، مرتب کردن داده‌ها یکی از کارهای خیلی رایجه. از مرتب کردن لیست مخاطبین توی گوشیتون بگیر تا مرتب کردن نتایج جستجو توی گوگل، همه جا یه جور الگوریتم مرتب‌سازی داره کار می‌کنه. مرتب سازی هرمی (Heap Sort) یکی از این الگوریتم‌هاست که یه سری ویژگی‌های خوب داره که باعث میشه توی بعضی شرایط انتخاب مناسبی باشه.

عملکرد نسبتاً خوب: در بیشتر موارد، سرعتش از الگوریتم‌های ساده‌تر مثل مرتب‌سازی حبابی (Bubble Sort) یا مرتب‌سازی درجی (Insertion Sort) خیلی بهتره.
مرتب‌سازی درجا (In-place): یعنی برای مرتب کردن داده‌ها، نیازی به حافظه اضافی زیادی نداره. این ویژگی، به خصوص وقتی با داده‌های حجیم سروکار داریم، خیلی مهمه.

خب، دیگه بریم سراغ اصل مطلب!

هرم چیه اصلا؟ (درخت هرمی - Heap Tree)

اولین قدم برای فهمیدن مرتب سازی هرمی (Heap Sort) اینه که بدونیم “هرم” یا همون “Heap” چیه. هرم یه نوع خاص از ساختار داده درختیه که ویژگی‌های زیر رو داره:

درخت دودویی کامل: یعنی تمام سطوح درخت پر هستند، به جز احتمالاً آخرین سطح که از چپ به راست پر میشه.

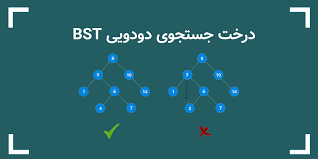
خاصیت هرمی: این خاصیت دو نوع داره:

هرم بیشینه (Max Heap): مقدار هر گره بزرگتر یا مساوی مقدار فرزندانشه. یعنی بزرگترین مقدار توی ریشه درخت قرار داره.
هرم کمینه (Min Heap): مقدار هر گره کوچکتر یا مساوی مقدار فرزندانشه. یعنی کوچیکترین مقدار توی ریشه درخت قرار داره.
توی مرتب سازی هرمی (Heap Sort)، معمولاً از هرم بیشینه استفاده می‌کنیم.

نمايش آرايه‌ای درخت هرمی

یه نکته خیلی مهم اینه که درخت هرمی رو میشه به راحتی توی یه آرایه ذخیره کرد. فرض کنید یه درخت هرمی داریم که توی یه آرایه به اسم arr ذخیره شده. اونوقت:

ریشه درخت، توی arr[0] قرار داره.
فرزند چپ گره arr[i]، توی arr[2*i + 1] قرار داره.
فرزند راست گره arr[i]، توی arr[2*i + 2] قرار داره.
والد گره arr[i]، توی arr[(i-1)/2] قرار داره.

این نمایش آرایه‌ای، خیلی کار رو برای پیاده‌سازی الگوریتم مرتب سازی هرمی (Heap Sort) راحت‌تر می‌کنه.

الگوریتم مرتب سازی هرمی (Heap Sort) قدم به قدم

حالا که فهمیدیم هرم چیه، وقتشه بریم سراغ خود الگوریتم مرتب سازی هرمی (Heap Sort). این الگوریتم دو مرحله اصلی داره:

ساختن هرم (Heapify): آرایه ورودی رو به یه هرم بیشینه تبدیل می‌کنیم.
مرتب‌سازی: به صورت مکرر بزرگترین عنصر (ریشه هرم) رو با آخرین عنصر آرایه جابجا می‌کنیم و بعد هرم رو دوباره تنظیم می‌کنیم (Heapify).

بیاید هر مرحله رو با جزئیات بیشتری بررسی کنیم:

1. ساختن هرم (Heapify)

فرض کنید یه آرایه نامرتب داریم. اولین کاری که باید بکنیم اینه که این آرایه رو به یه هرم بیشینه تبدیل کنیم. برای این کار، از آخرین گره غیربرگ شروع می‌کنیم و به سمت ریشه حرکت می‌کنیم. برای هر گره، تابع heapify رو صدا می‌زنیم. این تابع بررسی می‌کنه که آیا گره مورد نظر از فرزندانش کوچکتره یا نه. اگر کوچکتر بود، با بزرگترین فرزندش جابجا میشه و بعد تابع heapify رو برای فرزند جابجا شده دوباره صدا می‌زنیم تا خاصیت هرمی حفظ بشه.

پیاده‌سازی تابع heapify:

				
					def heapify(arr, n, i):
  """
  این تابع زیردرخت با ریشه i رو به یک هرم بیشینه تبدیل می‌کنه.
  n: اندازه آرایه
  i: اندیس ریشه زیردرخت
  """
  largest = i  # بزرگترین مقدار رو فرض می‌کنیم ریشه است
  l = 2 * i + 1     # اندیس فرزند چپ
  r = 2 * i + 2     # اندیس فرزند راست

  # اگر فرزند چپ بزرگتر از ریشه باشه
  if l < n and arr[i] < arr[l]:
    largest = l

  # اگر فرزند راست بزرگتر از بزرگترین مقدار فعلی باشه
  if r < n and arr[largest] < arr[r]:
    largest = r

  # اگر بزرگترین مقدار، دیگه ریشه نباشه
  if largest != i:
    # جابجایی
    arr[i], arr[largest] = arr[largest], arr[i]

    # Heapify کردن زیردرخت تحت تاثیر قرار گرفته
    heapify(arr, n, largest)

شرح کد:

largest = i: ابتدا فرض می‌کنیم که ریشه زیردرخت، بزرگترین مقدار رو داره.
l = 2 * i + 1 و r = 2 * i + 2: اندیس فرزندان چپ و راست رو محاسبه می‌کنیم.
if l < n and arr[i] < arr[l]: اگر فرزند چپ وجود داشته باشه (l < n) و مقدارش از ریشه بیشتر باشه، largest رو برابر l قرار می‌دیم.
if r < n and arr[largest] < arr[r]: اگر فرزند راست وجود داشته باشه (r < n) و مقدارش از بزرگترین مقدار فعلی (arr[largest]) بیشتر باشه، largest رو برابر r قرار می‌دیم.
if largest != i: اگر largest تغییر کرده باشه، یعنی یکی از فرزندان از ریشه بزرگتر بوده. در این صورت، ریشه رو با بزرگترین فرزند جابجا می‌کنیم و بعد تابع heapify رو برای زیردرخت تحت تاثیر قرار گرفته (همون زیردرختی که ریشه اش قبلا بزرگترین فرزند بوده) دوباره صدا می‌زنیم.

ساختن هرم از آرایه نامرتب:

حالا که تابع heapify رو داریم، می‌تونیم ازش برای ساختن هرم از یه آرایه نامرتب استفاده کنیم:

				
					def build_heap(arr):
  """
  این تابع یک آرایه نامرتب رو به یک هرم بیشینه تبدیل می‌کنه.
  """
  n = len(arr)

  # از آخرین گره غیربرگ شروع می‌کنیم و به سمت ریشه حرکت می‌کنیم
  for i in range(n // 2 - 1, -1, -1):
    heapify(arr, n, i)

شرح کد:

n = len(arr): اندازه آرایه رو به دست میاریم.
for i in range(n // 2 - 1, -1, -1): از آخرین گره غیربرگ (که اندیسش n // 2 - 1 هست) شروع می‌کنیم و به سمت ریشه (اندیس 0) حرکت می‌کنیم. این حلقه از آخر به اول حرکت می‌کنه.
heapify(arr, n, i): برای هر گره، تابع heapify رو صدا می‌زنیم.

2. مرتب‌سازی

بعد از اینکه آرایه رو به هرم بیشینه تبدیل کردیم، مرحله مرتب‌سازی شروع میشه. توی این مرحله، به صورت مکرر بزرگترین عنصر (که توی ریشه هرم قرار داره) رو با آخرین عنصر آرایه جابجا می‌کنیم. بعد از جابجایی، اندازه هرم رو یکی کم می‌کنیم (چون آخرین عنصر دیگه مرتب شده) و بعد دوباره تابع heapify رو برای ریشه صدا می‌زنیم تا هرم رو دوباره تنظیم کنیم. این کار رو تا وقتی که اندازه هرم به 1 برسه تکرار می‌کنیم.

پیاده‌سازی مرحله مرتب‌سازی:

				
					def heap_sort(arr):
  """
  این تابع یک آرایه رو با استفاده از الگوریتم مرتب سازی هرمی مرتب می‌کنه.
  """
  n = len(arr)

  # ساختن هرم
  build_heap(arr)

  # یک به یک عناصر رو از هرم استخراج می‌کنیم
  for i in range(n - 1, 0, -1):
    # جابجایی ریشه با آخرین عنصر
    arr[i], arr[0] = arr[0], arr[i]

    # Heapify کردن ریشه
    heapify(arr, i, 0)

شرح کد:

build_heap(arr): ابتدا آرایه رو به هرم بیشینه تبدیل می‌کنیم.
for i in range(n - 1, 0, -1): از آخرین عنصر آرایه (اندیس n - 1) شروع می‌کنیم و به سمت عنصر دوم (اندیس 1) حرکت می‌کنیم. این حلقه از آخر به اول حرکت می‌کنه.
arr[i], arr[0] = arr[0], arr[i]: ریشه هرم (بزرگترین عنصر) رو با آخرین عنصر آرایه جابجا می‌کنیم.
heapify(arr, i, 0): تابع heapify رو برای ریشه (اندیس 0) صدا می‌زنیم تا هرم رو دوباره تنظیم کنیم. اندازه هرم رو هم برابر i قرار می‌دیم، چون آخرین عنصر دیگه مرتب شده.

کد کامل مرتب سازی هرمی (Heap Sort) در پایتون

حالا می‌تونیم کد کامل الگوریتم مرتب سازی هرمی (Heap Sort) رو با هم ببینیم:

				
					def heapify(arr, n, i):
  largest = i
  l = 2 * i + 1
  r = 2 * i + 2

  if l < n and arr[i] < arr[l]:
    largest = l

  if r < n and arr[largest] < arr[r]:
    largest = r

  if largest != i:
    arr[i], arr[largest] = arr[largest], arr[i]
    heapify(arr, n, largest)


def build_heap(arr):
  n = len(arr)
  for i in range(n // 2 - 1, -1, -1):
    heapify(arr, n, i)


def heap_sort(arr):
  n = len(arr)
  build_heap(arr)
  for i in range(n - 1, 0, -1):
    arr[i], arr[0] = arr[0], arr[i]
    heapify(arr, i, 0)


# تست کد
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("آرایه مرتب شده:", arr)

تحلیل پیچیدگی زمانی و مکانی

پیچیدگی زمانی:
- بهترین حالت: O(n log n)
- متوسط حالت: O(n log n)
- بدترین حالت: O(n log n)
همونطور که می‌بینید، پیچیدگی زمانی مرتب سازی هرمی (Heap Sort) توی همه حالت‌ها یکسانه و برابر O(n log n) هست. این یعنی توی بدترین شرایط هم، عملکردش نسبتاً خوبه.
پیچیدگی مکانی:
- O(1)
مرتب سازی هرمی (Heap Sort) یه الگوریتم مرتب‌سازی درجا (In-place) هست، یعنی برای مرتب کردن داده‌ها، نیازی به حافظه اضافی زیادی نداره. به همین دلیل، پیچیدگی مکانیش O(1) هست.

مزایا و معایب مرتب سازی هرمی (Heap Sort)

مثل هر الگوریتم دیگه، مرتب سازی هرمی (Heap Sort) هم یه سری مزایا و معایب داره:

مزایا:

عملکرد خوب: پیچیدگی زمانی O(n log n) توی همه حالت‌ها.
مرتب‌سازی درجا (In-place): نیازی به حافظه اضافی زیادی نداره.
قابل پیش‌بینی: عملکردش توی همه حالت‌ها یکسانه.

معایب:

پیچیده‌تر از الگوریتم‌های ساده‌تر: درک و پیاده‌سازیش نسبت به الگوریتم‌هایی مثل مرتب‌سازی حبابی یا مرتب‌سازی درجی یکم سخت‌تره.
ناپایدار (Unstable): ممکنه ترتیب عناصر مساوی رو حفظ نکنه. (الگوریتم‌های پایدار، ترتیب عناصر مساوی رو حفظ می‌کنند.)

کاربردهای مرتب سازی هرمی (Heap Sort)

مرتب سازی هرمی (Heap Sort) توی شرایط مختلفی کاربرد داره:

وقتی حافظه محدوده: چون یه الگوریتم مرتب‌سازی درجا هست، برای مرتب کردن داده‌های حجیم توی سیستم‌هایی با حافظه محدود مناسبه.
وقتی به یه الگوریتم با عملکرد قابل پیش‌بینی نیاز داریم: چون پیچیدگی زمانیش توی همه حالت‌ها یکسانه، وقتی نیاز داریم که یه الگوریتم داشته باشیم که توی بدترین شرایط هم عملکرد قابل قبولی داشته باشه، می‌تونیم ازش استفاده کنیم.
پیاده‌سازی صف‌های اولویت (Priority Queues): هرم‌ها یکی از ساختارهای داده اصلی برای پیاده‌سازی صف‌های اولویت هستند.

مقایسه مرتب سازی هرمی (Heap Sort) با سایر الگوریتم‌های مرتب‌سازی

الگوریتم	پیچیدگی زمانی (بهترین)	پیچیدگی زمانی (متوسط)	پیچیدگی زمانی (بدترین)	پیچیدگی مکانی	پایدار؟
مرتب سازی هرمی	O(n log n)	O(n log n)	O(n log n)	O(1)	خیر
مرتب سازی سریع	O(n log n)	O(n log n)	O(n^2)	O(log n)	خیر
مرتب سازی ادغامی	O(n log n)	O(n log n)	O(n log n)	O(n)	بله
مرتب سازی درجی	O(n)	O(n^2)	O(n^2)	O(1)	بله
مرتب سازی حبابی	O(n)	O(n^2)	O(n^2)	O(1)	بله

همونطور که توی جدول می‌بینید، مرتب سازی هرمی (Heap Sort) از نظر پیچیدگی زمانی، عملکردی شبیه به مرتب سازی سریع (Quick Sort) و مرتب سازی ادغامی (Merge Sort) داره. اما مزیتش نسبت به مرتب سازی سریع اینه که توی بدترین حالت هم پیچیدگی زمانیش O(n log n) هست، در حالی که مرتب سازی سریع ممکنه توی بدترین حالت به O(n^2) برسه. از طرف دیگه، مرتب سازی ادغامی پایداره، ولی مرتب سازی هرمی (Heap Sort) ناپایداره. همچنین مرتب سازی ادغامی به حافظه اضافی نیاز داره، در حالی که مرتب سازی هرمی (Heap Sort) یه الگوریتم درجا هست.

جمع‌بندی

خب رفقا، امیدوارم این آموزش جامع و کامل مرتب سازی هرمی (Heap Sort) براتون مفید بوده باشه. سعی کردم با زبون خودمونی و با مثال و عکس، همه چیز رو بهتون توضیح بدم. مرتب سازی هرمی (Heap Sort) یه الگوریتم مرتب‌سازی قدرتمند و کاربردیه که توی شرایط مختلفی می‌تونه به کارتون بیاد. یادتون باشه که تمرین و تکرار، بهترین راه برای یادگیریه. پس دست به کد بشید و مرتب سازی هرمی (Heap Sort) رو پیاده‌سازی کنید و باهاش بازی کنید تا قشنگ ملکه ذهنتون بشه.

nivad

بازدید: