07
مهبستن
پروژه خود را از امروز شروع کنید91307930-021
فهرست مطالب
الگوریتم Floyd-Warshall
الگوریتم Floyd-Warshall یکی از الگوریتم‌های کلاسیک در علوم کامپیوتر است که برای حل مسئله یافتن کوتاه‌ترین مسیر بین تمام جفت‌های رأس‌ها در یک گراف جهت‌دار یا بدون جهت با وزن‌های لبه (مثبت یا منفی) استفاده می‌شود. این الگوریتم که به نام‌های رابرت فلوید و استفن وارشال نام‌گذاری شده است، در سال ۱۹۶۲ معرفی شد و به دلیل سادگی و کارایی‌اش در مسائل مختلف گراف، به یکی از الگوریتم‌های پرکاربرد تبدیل شده است. در این آموزش، به بررسی دقیق الگوریتم Floyd-Warshall، نحوه عملکرد آن، کاربردها، پیچیدگی زمانی و فضایی، و همچنین پیاده‌سازی‌های مختلف آن در زبان‌های برنامه‌نویسی خواهیم پرداخت.
الگوریتم Floyd-Warshall به دلیل توانایی‌اش در مدیریت گراف‌هایی با وزن‌های منفی (تا زمانی که چرخه منفی وجود نداشته باشد) و همچنین سادگی پیاده‌سازی، در بسیاری از مسائل علوم کامپیوتر و مهندسی مانند بهینه‌سازی شبکه‌ها، تحلیل ترافیک، و حتی در مسائل هوش مصنوعی کاربرد دارد. در ادامه، این الگوریتم را به صورت جامع و با جزئیات بررسی می‌کنیم.
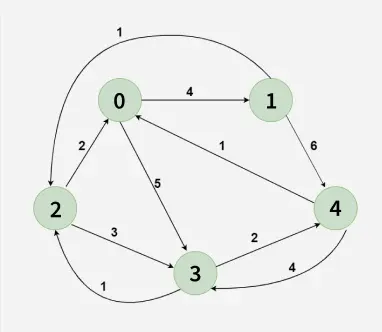
الگوریتم Floyd-Warshall چیست؟
الگوریتم Floyd-Warshall یک الگوریتم برنامه‌نویسی پویا (Dynamic Programming) است که برای یافتن کوتاه‌ترین مسیر بین تمام جفت‌های رأس‌ها در یک گراف وزنی استفاده می‌شود. برخلاف الگوریتم‌هایی مانند Dijkstra یا Bellman-Ford که برای یافتن کوتاه‌ترین مسیر از یک رأس مبدا به سایر رأس‌ها طراحی شده‌اند، الگوریتم Floyd-Warshall تمام مسیرهای ممکن بین هر جفت رأس را محاسبه می‌کند. این ویژگی باعث می‌شود که الگوریتم Floyd-Warshall برای گراف‌های متراکم یا گراف‌هایی که نیاز به محاسبه چندین مسیر کوتاه دارند، بسیار مناسب باشد.
الگوریتم Floyd-Warshall با استفاده از یک ماتریس فاصله (Distance Matrix) کار می‌کند که در آن هر عنصر نشان‌دهنده کوتاه‌ترین فاصله بین دو رأس است. این ماتریس در طی اجرای الگوریتم به‌روزرسانی می‌شود تا در نهایت کوتاه‌ترین مسیرهای ممکن را ارائه دهد.
اصول پایه الگوریتم Floyd-Warshall
ایده اصلی الگوریتم Floyd-Warshall این است که برای هر جفت رأس ((i, j))، بررسی کند که آیا با عبور از یک رأس واسطه ((k)) می‌توان مسیری کوتاه‌تر از مسیر فعلی بین ((i, j)) یافت یا خیر. این فرآیند به صورت تدریجی و با استفاده از یک رویکرد برنامه‌نویسی پویا انجام می‌شود.
ماتریس فاصله در الگوریتم Floyd-Warshall به صورت زیر تعریف می‌شود:
اگر بین دو رأس ((i, j)) لبه‌ای وجود داشته باشد، مقدار اولیه ماتریس برابر با وزن آن لبه است.
اگر لبه‌ای بین ((i, j)) وجود نداشته باشد، مقدار اولیه به بی‌نهایت (یا یک مقدار بسیار بزرگ) تنظیم می‌شود.
اگر (i = j) باشد، مقدار ماتریس برابر با صفر است (چون فاصله یک رأس تا خودش صفر است).
الگوریتم Floyd-Warshall این ماتریس را به‌روزرسانی می‌کند تا در نهایت، هر عنصر ((i, j)) نشان‌دهنده کوتاه‌ترین فاصله بین رأس‌های ((i, j)) باشد.
نحوه کار الگوریتم Floyd-Warshall
الگوریتم Floyd-Warshall از سه حلقه تو در تو استفاده می‌کند:
حلقه خارجی: برای انتخاب رأس واسطه ((k)).
حلقه میانی: برای انتخاب رأس مبدا ((i)).
حلقه داخلی: برای انتخاب رأس مقصد ((j)).
در هر مرحله، الگوریتم بررسی می‌کند که آیا مسیر از ((i)) به ((j)) با عبور از رأس ((k)) کوتاه‌تر از مسیر فعلی است یا خیر. اگر مسیر جدید کوتاه‌تر باشد، ماتریس فاصله به‌روزرسانی می‌شود.
مراحل الگوریتم Floyd-Warshall
مقداردهی اولیه:
یک ماتریس فاصله (dist) به اندازه (n \times n) (که (n) تعداد رأس‌هاست) ایجاد کنید.
مقادیر ماتریس را بر اساس وزن لبه‌ها پر کنید. اگر لبه‌ای وجود نداشته باشد، مقدار را به بی‌نهایت تنظیم کنید.
قطر اصلی ماتریس (جایی که (i = j)) را صفر قرار دهید.
به‌روزرسانی ماتریس فاصله:
برای هر رأس واسطه ((k))، تمام جفت‌های ((i, j)) را بررسی کنید.
اگر (dist[i][j] > dist[i][k] + dist[k][j])، مقدار (dist[i][j]) را به (dist[i][k] + dist[k][j]) تغییر دهید.
خروجی نهایی:
پس از اتمام حلقه‌ها، ماتریس (dist) حاوی کوتاه‌ترین فاصله بین تمام جفت‌های رأس‌ها خواهد بود.
شبه‌کد الگوریتم Floyd-Warshall
function FloydWarshall(graph):
n = تعداد رأس‌های گراف
dist = ماتریس n × n با مقداردهی اولیه بر اساس وزن لبه‌ها
for k from 1 to n:
for i from 1 to n:
for j from 1 to n:
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
return dist
پیچیدگی زمانی و فضایی الگوریتم Floyd-Warshall
پیچیدگی زمانی
الگوریتم Floyd-Warshall از سه حلقه تو در تو استفاده می‌کند که هر کدام (n) بار اجرا می‌شوند (که (n) تعداد رأس‌های گراف است). بنابراین، پیچیدگی زمانی الگوریتم به صورت زیر است:
پیچیدگی زمانی: (O(n^3))
این پیچیدگی نشان می‌دهد که الگوریتم Floyd-Warshall برای گراف‌های کوچک تا متوسط بسیار مناسب است، اما برای گراف‌های بسیار بزرگ ممکن است کند باشد.
پیچیدگی فضایی
الگوریتم Floyd-Warshall از یک ماتریس (n \times n) برای ذخیره فاصله‌ها استفاده می‌کند. بنابراین:
پیچیدگی فضایی: (O(n^2))
اگر بخواهیم مسیرهای کوتاه‌ترین را نیز ذخیره کنیم (نه فقط فاصله‌ها)، به یک ماتریس اضافی برای ذخیره رأس‌های واسطه نیاز داریم که باز هم پیچیدگی فضایی را (O(n^2)) نگه می‌دارد.
مزایا و معایب الگوریتم Floyd-Warshall
مزایا
سادگی پیاده‌سازی: الگوریتم Floyd-Warshall کد نسبتاً ساده‌ای دارد و به راحتی قابل پیاده‌سازی است.
پشتیبانی از وزن‌های منفی: برخلاف الگوریتم دایکسترا، الگوریتم Floyd-Warshall می‌تواند گراف‌هایی با وزن‌های منفی را مدیریت کند (تا زمانی که چرخه منفی وجود نداشته باشد).
یافتن تمام مسیرهای کوتاه: این الگوریتم تمام مسیرهای کوتاه بین هر جفت رأس را به طور همزمان محاسبه می‌کند.
مناسب برای گراف‌های متراکم: الگوریتم Floyd-Warshall برای گراف‌هایی که تعداد لبه‌ها نزدیک به (n^2) است، بسیار کارآمد است.
معایب
پیچیدگی زمانی بالا: به دلیل پیچیدگی (O(n^3))، این الگوریتم برای گراف‌های بسیار بزرگ مناسب نیست.
نیاز به حافظه زیاد: ماتریس فاصله (n \times n) برای گراف‌های بزرگ حافظه زیادی مصرف می‌کند.
عدم توانایی در مدیریت چرخه‌های منفی: اگر گراف دارای چرخه منفی باشد، الگوریتم Floyd-Warshall نمی‌تواند به درستی کار کند.
کاربردهای الگوریتم Floyd-Warshall
الگوریتم Floyd-Warshall در بسیاری از حوزه‌ها کاربرد دارد، از جمله:
شبکه‌های ارتباطی: برای یافتن کوتاه‌ترین مسیر در شبکه‌های مخابراتی یا اینترنتی.
تحلیل ترافیک: برای محاسبه بهترین مسیرها در سیستم‌های حمل‌ونقل.
گراف‌های اجتماعی: برای تحلیل روابط بین افراد در شبکه‌های اجتماعی.
هوش مصنوعی: در مسائل بهینه‌سازی که نیاز به محاسبه مسیرهای کوتاه دارند.
گراف‌های وزنی منفی: در مسائل مالی یا اقتصادی که ممکن است وزن‌های منفی وجود داشته باشد.
پیاده‌سازی الگوریتم Floyd-Warshall در زبان‌های برنامه‌نویسی
برای درک بهتر الگوریتم Floyd-Warshall، در ادامه پیاده‌سازی این الگوریتم را در چند زبان برنامه‌نویسی ارائه می‌دهیم.
پیاده‌سازی در پایتون
پایتون به دلیل سادگی و خوانایی، یکی از بهترین زبان‌ها برای پیاده‌سازی الگوریتم Floyd-Warshall است.
def floyd_warshall(graph):
n = len(graph)
# ایجاد ماتریس فاصله و کپی مقادیر اولیه
dist = [[float('inf')] * n for _ in range(n)]
# مقداردهی اولیه ماتریس فاصله
for i in range(n):
for j in range(n):
dist[i][j] = graph[i][j]
# به‌روزرسانی ماتریس فاصله
for k in range(n):
for i in range(n):
for j in range(n):
if dist[i][k] != float('inf') and dist[k][j] != float('inf'):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
return dist
# مثال استفاده
graph = [
[0, 5, float('inf'), 10],
[float('inf'), 0, 3, float('inf')],
[float('inf'), float('inf'), 0, 1],
[float('inf'), float('inf'), float('inf'), 0]
]
result = floyd_warshall(graph)
for row in result:
print(row)
پیاده‌سازی در سی‌پلاس‌پلاس
در سی‌پلاس‌پلاس، الگوریتم Floyd-Warshall به صورت زیر پیاده‌سازی می‌شود:
#include <iostream>
#include <vector>
using namespace std;
const int INF = 1e9;
vector<vector<int>> floyd_warshall(vector<vector<int>>& graph) {
int n = graph.size();
vector<vector<int>> dist = graph;
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != INF && dist[k][j] != INF) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
return dist;
}
int main() {
vector<vector<int>> graph = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
auto result = floyd_warshall(graph);
for (const auto& row : result) {
for (int val : row) {
if (val == INF) cout << "INF ";
else cout << val << " ";
}
cout << endl;
}
return 0;
}
پیاده‌سازی در جاوا
پیاده‌سازی الگوریتم Floyd-Warshall در جاوا به صورت زیر است:
public class FloydWarshall {
static final int INF = Integer.MAX_VALUE / 2;
public static int[][] floydWarshall(int[][] graph) {
int n = graph.length;
int[][] dist = new int[n][n];
// مقداردهی اولیه
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = graph[i][j];
}
}
// به‌روزرسانی ماتریس فاصله
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != INF && dist[k][j] != INF) {
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
return dist;
}
public static void main(String[] args) {
int[][] graph = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
int[][] result = floydWarshall(graph);
for (int[] row : result) {
for (int val : row) {
if (val == INF) System.out.print("INF ");
else System.out.print(val + " ");
}
System.out.println();
}
}
}
تشخیص چرخه‌های منفی با الگوریتم Floyd-Warshall
یکی از قابلیت‌های جالب الگوریتم Floyd-Warshall، توانایی تشخیص چرخه‌های منفی در گراف است. اگر پس از اجرای الگوریتم، هر یک از مقادیر قطر اصلی ماتریس فاصله (یعنی (dist[i][i])) منفی باشد، این نشان‌دهنده وجود یک چرخه منفی در گراف است. دلیل آن این است که یک چرخه منفی باعث می‌شود فاصله یک رأس تا خودش کاهش یابد، که غیرممکن است مگر اینکه چرخه‌ای با مجموع وزن منفی وجود داشته باشد.
برای تشخیص چرخه منفی، می‌توان کد زیر را به پیاده‌سازی پایتون اضافه کرد:
def has_negative_cycle(dist):
n = len(dist)
for i in range(n):
if dist[i][i] < 0:
return True
return False
بازسازی مسیر در الگوریتم Floyd-Warshall
برای بازسازی مسیرهای کوتاه‌ترین، می‌توان یک ماتریس اضافی به نام (next) ایجاد کرد که رأس بعدی در مسیر کوتاه‌ترین از ((i)) به ((j)) را ذخیره می‌کند. این ماتریس در حین اجرای الگوریتم Floyd-Warshall به‌روزرسانی می‌شود.
پیاده‌سازی با بازسازی مسیر
def floyd_warshall_with_path(graph):
n = len(graph)
dist = [[float('inf')] * n for _ in range(n)]
next_vertex = [[None] * n for _ in range(n)]
# مقداردهی اولیه
for i in range(n):
for j in range(n):
dist[i][j] = graph[i][j]
if graph[i][j] != float('inf') and i != j:
next_vertex[i][j] = j
# به‌روزرسانی ماتریس فاصله و مسیر
for k in range(n):
for i in range(n):
for j in range(n):
if dist[i][k] != float('inf') and dist[k][j] != float('inf'):
if dist[i][j] > dist[i][k] + dist[k][j]:
dist[i][j] = dist[i][k] + dist[k][j]
next_vertex[i][j] = next_vertex[i][k]
return dist, next_vertex
def get_path(next_vertex, start, end):
if next_vertex[start][end] is None:
return []
path = [start]
while start != end:
start = next_vertex[start][end]
path.append(start)
return path
# مثال استفاده
graph = [
[0, 5, float('inf'), 10],
[float('inf'), 0, 3, float('inf')],
[float('inf'), float('inf'), 0, 1],
[float('inf'), float('inf'), float('inf'), 0]
]
dist, next_vertex = floyd_warshall_with_path(graph)
path = get_path(next_vertex, 0, 3)
print("Shortest path from 0 to 3:", path)
بهینه‌سازی الگوریتم Floyd-Warshall
الگوریتم Floyd-Warshall به طور کلی بسیار بهینه است، اما در موارد خاص می‌توان بهینه‌سازی‌هایی انجام داد:
کاهش فضای ذخیره‌سازی: اگر فقط به ماتریس فاصله نیاز باشد و مسیرها مهم نباشند، می‌توان از یک ماتریس به جای دو ماتریس استفاده کرد.
موازی‌سازی: حلقه‌های الگوریتم را می‌توان با استفاده از تکنیک‌های موازی‌سازی (مانند GPU یا چندپردازشی) بهبود داد.
استفاده از بیت‌ست برای گراف‌های خاص: در گراف‌هایی با وزن‌های کوچک، می‌توان از نمایش بیت‌ست برای کاهش مصرف حافظه استفاده کرد.
مقایسه الگوریتم Floyd-Warshall با سایر الگوریتم‌ها
الگوریتم Floyd-Warshall در مقایسه با الگوریتم‌های دیگر مانند Dijkstra و Bellman-Ford تفاوت‌های کلیدی دارد:
Dijkstra: برای یافتن کوتاه‌ترین مسیر از یک رأس مبدا به تمام رأس‌ها استفاده می‌شود و نمی‌تواند وزن‌های منفی را مدیریت کند. پیچیدگی زمانی آن (O(V^2)) یا (O((V + E) \log V)) با استفاده از هیپ است.
Bellman-Ford: برای یافتن کوتاه‌ترین مسیر از یک رأس مبدا استفاده می‌شود و می‌تواند وزن‌های منفی را مدیریت کند، اما پیچیدگی زمانی آن (O(VE)) است.
Floyd-Warshall: تمام مسیرهای کوتاه را محاسبه می‌کند و وزن‌های منفی را پشتیبانی می‌کند، اما پیچیدگی زمانی_unspecified
System: زمانی آن (O(n^3)) است.
نتیجه‌گیری
الگوریتم Floyd-Warshall یک ابزار قدرتمند و ساده برای حل مسئله کوتاه‌ترین مسیر بین تمام جفت‌های رأس‌ها در گراف‌های وزنی است. این الگوریتم به دلیل سادگی، توانایی مدیریت وزن‌های منفی، و محاسبه همزمان تمام مسیرهای کوتاه، در بسیاری از مسائل کاربرد دارد. با این حال، برای گراف‌های بسیار بزرگ ممکن است به دلیل پیچیدگی زمانی بالا مناسب نباشد. در این آموزش، به بررسی کامل الگوریتم Floyd-Warshall، نحوه کار آن، پیاده‌سازی‌ها، و کاربردهای آن پرداختیم. امیدواریم این آموزش به شما در درک بهتر این الگوریتم کمک کرده باشد.
بیشتر بخوانید:”فورتی آنالایز و قابلیت های آن“
دیدگاه بگذارید